���ԂƂ��Ƃ�ދ��ȉ�c�������āA�ɂԂ��Ƃ��Ď��삵�Ď����ʼn��������ł��B
�@�w�n�t�@�{�@�`�q�d�@���@�h�b�j�x�@�i�R��+�R�����S���j�s�g�x�@�{�@�`�q�d�@���@�h�c�n�k�i�R��+�R�����S���j�P�O���ׂĈႤ�����i�����Z�j�̕��ʎZ�B
�܂�A�O�|�X�̐��l���d�������������܂��B
�f��̎������S�P�^�̎��R���u
�h�b�j�x�@
�h�c�n�k�v�@�ɂ��āA
�@��P�F�@�ŏ��l�����߂�B
�@��Q�F�@�ő�l�����߂�B
�@��R�F�@�\�Șa�����ʂ肠�邩�����߂�B
�@�i�u
�h�b�j�x�@
�h�c�n�k�v�����ɂ��Ă̂ݐ����Ă��������B�j
��P�E�Q�E�R�@�S�ā@�����ĂɌN�����܂��B
��P�E�Q�͔��p�S���̐����ŁA��R�͉������m��܂����p�ŁB
�@12/2�@19�F30�@�@�x�������܂�������P�O�S���Ⴄ�����Ƃ����̂���|�ł��̂ŁA����ɉ����Ăł��������������B���}���x�������w�ɕς��Ă����܂����A���ɏ�肢�V�������v�������當���g�S�̂�ς��邩������܂���B12/3�@22�F30�@�@�s�g�x�@�{�@�`�q�d�@���@�h�c�n�k�@�u���̓A�C�h���v�ɕς��܂����B
��������͈�ؖ{���I�Ȗ��ł͂Ȃ��āA10�S���Ⴄ�����ł���Ƃ������Ƃ��������̖����������߂̃|�C���g�ł��B����݂Ԃ��ł��Ȃ�Ƃ���������Ȃ̂ł����ǁA���������ł��̂ł�������������@���Љ�����B12/6���ɍl�����̃q���g�𓊓��\��@�@>>34�P�S���i���j����ڏ��Ɍ��J�\��ł��@12/11 22:00 j
j 




 ��
��


 ��
�� �݂ꂢ
�݂ꂢ 




 error
error 





 �X�[�p�[���[��
�X�[�p�[���[�� 
 �܂�
�܂� 

 ������
������ 


 HYF
HYF 

 �R�R�m�J
�R�R�m�J 
 s_hskz
s_hskz 


 ��
��
 ��
��


 ��
��

 �����̂�
�����̂� 

 �҂��
�҂�� 
 Yss
Yss 














 ���ʏ����h�L�b�I
���ʏ����h�L�b�I











 �@�@
�@�@ �ԈႢ�ɋC�Â��܂����B�o�����܂�m(_ _)m
�ԈႢ�ɋC�Â��܂����B�o�����܂�m(_ _)m �����e���Ǝv������߂��Ȃ��̂���������Ȃ̂ł��I�i����A�����炢����
�����e���Ǝv������߂��Ȃ��̂���������Ȃ̂ł��I�i����A�����炢����  �j�j
�j�j




 �Z���E���w�N�C�Y
�Z���E���w�N�C�Y �Z���E���w�N�C�Y
�Z���E���w�N�C�Y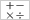 �v�Z
�v�Z ���H���E���ʎZ
���H���E���ʎZ