���̃N�C�Y�̃q���g
-
�q���g�m��Ȃ���
���̃N�C�Y�̎Q���ҁi23�l�j
 �g��
�g��
�@
 ���F�����
���F�����
�@

 �A�g
�A�g
�@



 KID
KID
�@
 QQQQQ
QQQQQ
�@
 �S�q
�S�q
�@ �� �r�`�m
�r�`�m
�@
 �y�q�j�R
�y�q�j�R
�@
 ���낤
���낤
�@
 visnu
visnu
�@
 masuda43
masuda43
�@
 �R���R��
�R���R��
�@
 ����
����
�@
 ���h�s�[
���h�s�[
�@

 neri
neri
�@
 �ς�
�ς�
�@
 �`��
�`��
�@
 �j�x�n
�j�x�n
�@
 chupie
chupie
�@
 �n���o�[�K�[
�n���o�[�K�[
�@
 �Ȃ݂�����
�Ȃ݂�����
�@

 yuu\
yuu\
�@
 IPON
IPON
�@
�W�������E�L�[���[�h
�g�їp�y�[�W

�g�ѓd�b��QR�R�[�h�ǂݎ��@�\�ł��̃y�[�W�������܂��B
�L��

�L��
�L��
�L��
�L��
�N�C�Y�嗤�֘A����





 �S�d�̉~�̌����
�S�d�̉~�̌����


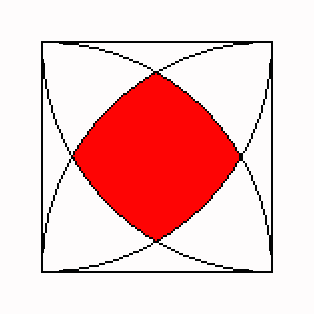





 �E�E�Ђ���Ƃ��Ă����������Ƃł��傤���H
�E�E�Ђ���Ƃ��Ă����������Ƃł��傤���H 




 �ӂЂギ
�ӂЂギ
 �ł�
�ł�




 �Z���E���w�N�C�Y
�Z���E���w�N�C�Y �Z���E���w�N�C�Y
�Z���E���w�N�C�Y