

|

|
 ツイート
ツイート
|
 正三角形に内接する正方形 正三角形に内接する正方形
難易度:★★

問題だけ思いついたときは難易度☆4くらいに思えたのに、いざ計算してみたら意外と程よい難易度。
正方形が正三角形に内接しています。 (1)正三角形の一辺の長さに対して正方形の一辺の長さが最小であるとき、 正三角形と正方形の一辺の長さの比を求めてください。 (2)正三角形の一辺の長さに対して正方形の一辺の長さが最大であるとき、 正三角形と正方形の一辺の長さの比を求めてください。 この問題の「内接」の定義と、配置の例を以下に示します。 定義 : ・正三角形のすべての辺上に、正方形の頂点が1つ以上ずつある ・正方形は、正三角形内に完全に収まっている (※追加条件 2019/11/19 3:00) 配置例 : 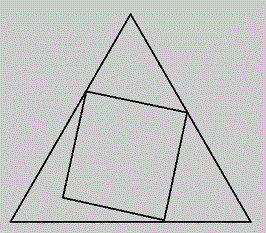 (正三角形の辺上に無い正方形の頂点が、1つまで存在してもよい)
|

回答募集は終了しました。





 )
)
 算数・数学クイズ
算数・数学クイズ 算数・数学クイズ
算数・数学クイズ 計算
計算 図形パズル
図形パズル