算数/数学クイズ答え

Q5の答え

下記参照

正解者
kaitoさん yoshiさん	croissantさん

解説

＝＝＝＝＝出題者より＝＝＝＝＝

(1)
下の図のように、正三角形の形に「1」をn段ならべます。

1
1 1
1 1 1
.
.
.
1 1 ........ 1 1　　n個

この合計がSaとなることはわかると思います。
これと同じ正三角形をひっくり返して横にならべてくっつけます。

1　　　　1 1 ........ 1 1
1 1 1 1 1
1 1 1
. .
. .
. 1 1
1 1 ........ 1 1　 1

隙間なくくっつけると底辺がn+1、高さがnの平行四辺形になりますので、
この合計はn(n+1)です。正三角形2個分ですから2Saです。
2Sa=n(n+1)すなわち　Sa=n(n+1)/2となります。

(2)
下の図のように、正三角形の形に1からnまでをn段ならべます。

1
2 2
3 3 3
.
.
.
n n ........ n n　　n個

これを上から全部足していくと、
1×1+2×2+.......+n×nということになりますので、求めるSbになります。

また、この数値の個数(合計ではありません)は(1)より、n(n+1)/2個です。

この正三角形をまず、時計回りに120°回転します。

n
n n-1
n n-1 n-2
.
.
.
n n ........ 2 1

となります。もう一回時計回りに120°回転します。

n
n-1 n
n-2 n-1 n
.
.
.
1 2 ........ n-1 n
となります。この三つの正三角形を、紙を重ねるように重ね合わせます。
すると、重なった数値の合計は、あら不思議、すべて2n+1となっています。
数値の個数は前述の通りn(n+1)/2ですから、すべての合計は、
n(n+1)(2n+1)/2です。正三角形3個分ですから3Sbのはずです。
3Sb=n(n+1)(2n+1)/2 すなわち　Sb=n(n+1)(2n+1)/6ということがわかります。

◆croissantさんの解答

Saの問題は、天才数学者ガウスが子供の頃に見つけた解法で有名ですね。

↑○
　○○
ｎ○○○
　｜　　＼
↓○○○○○
　←　ｎ　→
1＋2＋3＋…＋n

↑○●●●●●
　○○＼　　｜
ｎ○○○●●●
　｜　　＼●●
↓○○○○○●
　← ｎ＋１ →
2×(1＋2＋3＋…＋n)＝n×(n＋1)なので、
Sa＝1＋2＋3＋…＋n＝n×(n＋1)÷2

Sbの問題は、右辺がnの3次関数であることからSaの考え方を3次元に拡張して、
また、右辺の「1／6」にヒントを得て、
「立方体を対角線（？）で6つの4角錐に分割する」方法を、
小学生向けに積み木を使って説明してみました。

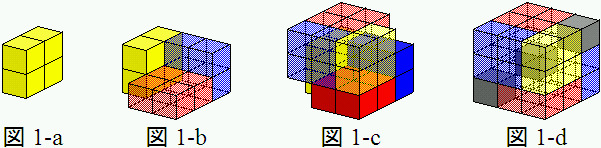
まず、一辺1cmの立方体を2×2＝4個くっつけた板を単位として（図1-a）、
3cm×3cm×3cmの空間に6単位を詰めると（図1-b, -c）、
3×3×3−4×6＝3で3個の立方体の分だけ空間が残ります（図1-d、灰色の部分）。



次は、同じく一辺1cmの立方体を4×4＝16個くっつけた板を単位として、
この様に出来上がった3cm×3cm×3cmの物体を中心にして、
5cm×5cm×5cmの空間を埋めるように6面に板を貼り付けます（図2-a, -b）。
やはり、2箇所の角に空間が残ります（図2-c）。



以降、同様に、板を2i×2i個の立方体に増やしながら、
(2i＋1)cm×(2i＋1)cm×(2i＋1)cmの空間を埋めるように
合計n回6面に貼り付け続けると、
(2n＋1)cm×(2n＋1)cm×(2n＋1)cmの空間のうち、
左下から右上にかけて、対角線（？）上に合計(2n+1)この空間が残ります（図3、n=3の場合）。



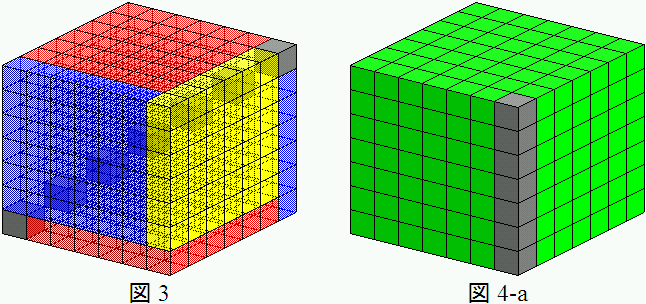
ここで、立方体の総数を調べます。
図3の、(2n＋1)個の空白を、一行に集めてみます（図4-a）。
図4-bのように分割すると、4等分出来ることが分かります。
ですから、
(2n＋1)×(2n＋1)×(2n＋1)−(2n＋1)＝4×n×(n＋1)×(2n＋1) …（式1）
となりました。



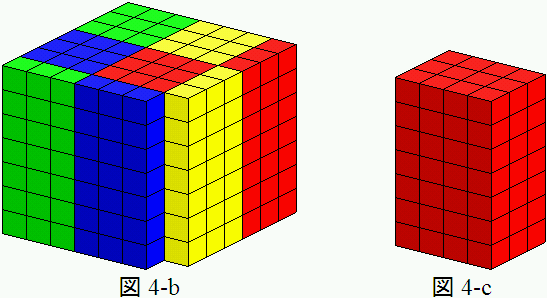
先程の形（図3）に戻って、中心より下の赤い立方体に注目します。
階段ピラミッドのようなこの形状は、
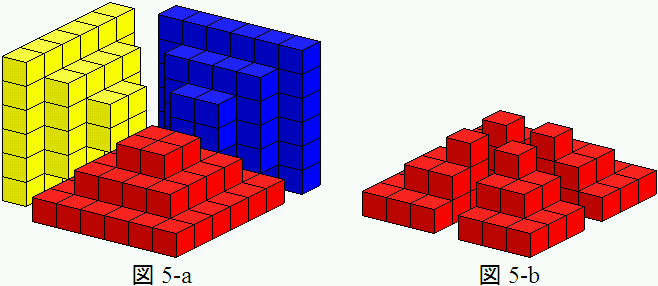
先程の形（図3）の6分の1であることが分かります（図5-a）。
更に、この階段ピラミッドを4等分すると、
(1×1＋2×2＋…＋n×n)個の立方体であることが分かります（図5-b）。
つまり、
(2n＋1)×(2n＋1)×(2n＋1)−(2n＋1)＝6×4×(1×1＋2×2＋…＋n×n) …（式2）



これで準備が整いました。式1と式2から、
6×4×(1×1＋2×2＋…＋n×n)＝4×n×(n＋1)×(2n＋1)なので、
Sb＝1×1＋2×2＋…＋n×n＝n×(n＋1)×(2n＋1)÷6

以上、証明終了です。

◆yoshiさんの解答

算数ではn(n+1)などという数式は用いないため証明できない。
算数のレベルだとこの場合n×(n+1)となる。
かなりひねくれててすいません＾＾；

参考

我々は必ずこの島を守り抜く。浜辺で戦い、飛行場で戦い、野原で、街頭で戦い、丘陵で戦い、決して屈服しない。 -- Winston Churchill

問題投稿者：PDJさん

[問題に戻る] -- [算数/数学クイズ目次] -- [次の問題へ進む]