クイズ&パズル答え
クイズ大陸トップ > Q166~Q170 > A166
Q166の答え下記参照
正解者
 |
JOKERさん
Otsuka Yusukeさん
みるくここあさん
レモンソテーさん
にんげさん
okyonさん
|
You taharaさん
ikezakiさん
キングナッツさん
ギアゴーレムさん
0系さん
nishiさん
|
◆解説◆
一筆書き・・みなさんも子供のころ一度はハマったことがあるのではないでしょうか。じつはこの一筆書きには、法則があることをご存知ですか?自分はまったく知りませんでしたが・・(^.^;)
=====一筆書き判別法=====
☆以下の条件のどちらかが成り立つときのみ一筆書きできる
・すべての頂点の次数(頂点から出ている線の数)が偶数
・次数が奇数の頂点の数が2で、残りの頂点の次数は全て偶数
次数が奇数である頂点(ノード)は、一筆書きの始点か終点でなければならず、したがって奇数点をもつノードが3つ以上ある図は一筆書きできない
=================
この定理は、数学界では有名なレオンハルト・オイラーによるもので、ネットワークの問題などを考える上では基本的な考え方となっているようです。
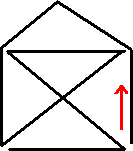 ←Q166解答例 ←Q166解答例
ご覧のとおり、今回の図もこの判別法がうまくあてはまっていますよネo(^-^*)o
◆0系さんの解答
解答例3種です

◆レモンソテーさん他の解答
はじめまして。流れ着いて、ついついクイズにハマりました。
たまにこういうのに挑戦してみるとマジでおもしろいですね。
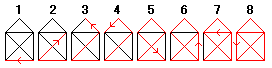
◆Otsuka Yusukeさんの解答
一筆書きのクイズなんですが、
奇数のノードから始まって奇数のノードで終わればいいのですね。
奇数のノードが3個以上の場合には解けません。0の時は解けますね
◆You taharaさんの解答
三角形五つに分けて、三角形の1つずつの角に番号をつけて答えます。
解りにくいかもしれませんが・・・
まず、真ん中の点を1とします。そして右下の点を2、
その左側の点を3、その上を4、頂点を5、最後の点を6とすると、
3,2,1,3,4,1,6,4,5,6,2(解答例の1つ)
の順でたどっていけば、一筆書きができます
暇がある方は、応用問題を掲載しておきますので考えてみて下さい。
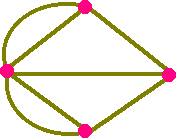
これは『ケーニヒスベルクの問題』として知られています。
どうがんばっても一筆では不可能なんですが・・(^.^;)
しかし、たとえば以下のような似た図なら一筆書きできます。
条件をしっかり満たしていることが分かりますね
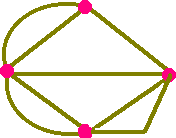 画像提供:You taharaさん
画像提供:You taharaさん
大切なのは結果じゃない 今何のために生きているか
何を作り出すことができたのか 守るべきものは何なのか
生きている間に人がその答えを見つけ出すことができれば
それでいいんじゃないのか? --- [Square / Final FantasyⅥ]
問題:大嶋さんより提供頂きました
| 
 ←Q166解答例
←Q166解答例


 画像提供:You taharaさん
画像提供:You taharaさん