ｸｲｽﾞ大陸
ビリオンズ
問題文を読む(773 文字)
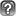 ﾋﾝﾄ | 【線分の長さとかは実際どーでもいいんです。】 |
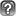| ﾋﾝﾄ | 【αとβを比べるとき、直接じゃなくてもαとγ,βとγをそれぞれ比べればいいのです。】 |
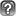| ﾋﾝﾄ | 【直線ACと直線BDの交点を使うといいですよ。】 |
| ◎解答・解説 | 【正解は③同じ 解答例： 直線CAと直線DBの交点を点Eとします。 この時、線分AB上の任意の点を点Fとし、直線EFを考えます。 Eは定点ですので、直線EFは点Fによって決定されます。 つまり、１つの点Fに対し1つの直線EFができるわけです。 よって点Fの数即ち線分AB上の点の数は、直線EFの数即ち点Eと線分ABを通る直線の数と等しいと言えます。 線分CDにおいても同様のことが言えます。 まとめますと、線分AB上の点の数は点Eと線分ABを通る直線の数に等しく、線分CD上の点の数は点Eと線分CDを通る直線の数に等しくなるわけです。 ここで点Eと線分ABを通る直線と、点Eと線分CDを通る直線は、A,C,Eが一直線上にあり、B,D,Eも一直線上にあるため、どちらも同じ範囲を動きます。 よって、点Eと線分ABを通る直線の数と、点Eと線分CDを通る直線の数は等しいといえます。 したがって、線分AB上の点の数と線分CD上の点の数は等しいとみなすことができるのです。 ※数学があまり得意でない方にも分かるようできるだけ分かりやすく書いたつもりです。 ※疑問・質問などあったら聞いてください。 ちなみにこの考え方を用いると異なる２点を結ぶ線分上の点の数はすべて等しいとみなすことができます。 あと、ボムボムさんのような解答も考えられます。解法としてはほぼ同じです。】 |
ﾋﾝﾄが3つあるよ
スローガン：囁き欄あり（答えがわかったら皆に内緒で囁いてね！）
ロック中につき閲覧専用となってます| Page: 1 | 2 | 3 | 4 | |
| Page: 1 | 2 | 3 | 4 | |
問題へジャンプ
みにすとりーと (168 文字)