崱夞偼傎傫偺彮偟擄偟偄偐傕丠
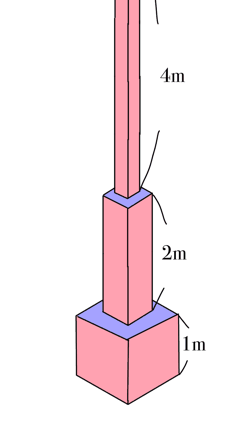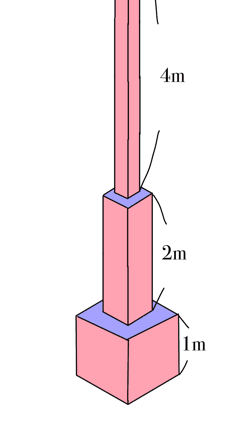
恾偺傛偆側暔懱偵偮偄偰峫偊傞丅
恾偺暔懱偼丄壓偵偁傞捈曽懱偺丄崅偝傪擇攞偵偟偰丄廲偲墶偺挿偝傪擇暘偺堦攞偟偨捈曽懱傪師乆偲柍尷偵慻傒崌傢偣偰偄偭偨暔懱偱偁傞丅
傑偨丄堦斣壓偵偼丄1m亊1m亊1m偺棫曽懱偑偁傞丅(愢柧壓庤偱偛傔傫側偝偄)
偙偙偱丄偙偺暔懱偺柺愊偼愒+惵偺柺愊側偺偱(掙柺偼惵偲峫偊傞)...嘆
惵偺柺愊偼丄
1+乷(1亊1-0.5亊0.5)+(0.5亊0.5-0.25亊0.25)+...乸
=1+1=2...嘇
愒偺柺愊偼丄
4亊乷1亊1+2亊0.5+4亊0.25+8亊0.125+...乸
=4亊乷1+1+1+1+...乸
=亣...嘊
傛偭偰丄暔懱偺柺愊偼丄2+亣=亣...嘋
偝傜偵丄懱愊偵偮偄偰峫偊傞丅柺愊偑柍尷偱懱愊偑桳尷偺暔懱傪峫偊傞偲丄懱愊偑桳尷側偺偱偙偺暔懱偼幚尰壜擻偲偄偆偙偲偵側傞偑丄柺愊偑柍尷偺暔懱偼懚嵼偟側偄偺偱丄懱愊偼柍尷偲側傞丅(懱愊偑柍尷偺暔懱偼懚嵼偟側偄)
暔懱偺懱愊傪V偲偡傞偲丄
V=亣...嘍
傑偨丄恾傛傝懱愊傪媮傔傞偲丄
V=(1亊1亊1)+(2亊0.5亊0.5)+(4亊0.25亊0.25)+...
=1+0.5+0.25+.....
=2...嘐
傛偭偰丄亣=2...嘑
椉曈亣偱妱偭偰丄
1=0...嘒
椉曈偵1傪懌偟偰丄
2=1...嘓
Q.E.D. 徹柧廔椆
摉慠偙偺寢壥偼偍偐偟偄偱偡偑丄偙偺傛偆側寢壥偵側偭偨尨場偼偙偺徹柧偺偳偙偱偟傚偆偐丅偦偺売強傪嘆偐傜嘓偺偆偪堦偮慖傫偱壓偝偄丅
壣側恖偼棟桼傕偍婅偄偟傑偡丅
掲傔愗傝偼堦廡娫丅
捛婰
惵偺柺愊偲愒偺柺愊偺搑拞寁嶼偑晛捠偵娫堘偊偰偨偺偱廋惓偟傑偟偨丅偡傒傑偣傫丅摎偊偼曄峏側偟偱偡丅

恾偺傛偆側暔懱偵偮偄偰峫偊傞丅
恾偺暔懱偼丄壓偵偁傞捈曽懱偺丄崅偝傪擇攞偵偟偰丄廲偲墶偺挿偝傪擇暘偺堦攞偟偨捈曽懱傪師乆偲柍尷偵慻傒崌傢偣偰偄偭偨暔懱偱偁傞丅
傑偨丄堦斣壓偵偼丄1m亊1m亊1m偺棫曽懱偑偁傞丅(愢柧壓庤偱偛傔傫側偝偄)
偙偙偱丄偙偺暔懱偺柺愊偼愒+惵偺柺愊側偺偱(掙柺偼惵偲峫偊傞)...嘆
惵偺柺愊偼丄
1+乷(1亊1-0.5亊0.5)+(0.5亊0.5-0.25亊0.25)+...乸
=1+1=2...嘇
愒偺柺愊偼丄
4亊乷1亊1+2亊0.5+4亊0.25+8亊0.125+...乸
=4亊乷1+1+1+1+...乸
=亣...嘊
傛偭偰丄暔懱偺柺愊偼丄2+亣=亣...嘋
偝傜偵丄懱愊偵偮偄偰峫偊傞丅柺愊偑柍尷偱懱愊偑桳尷偺暔懱傪峫偊傞偲丄懱愊偑桳尷側偺偱偙偺暔懱偼幚尰壜擻偲偄偆偙偲偵側傞偑丄柺愊偑柍尷偺暔懱偼懚嵼偟側偄偺偱丄懱愊偼柍尷偲側傞丅(懱愊偑柍尷偺暔懱偼懚嵼偟側偄)
暔懱偺懱愊傪V偲偡傞偲丄
V=亣...嘍
傑偨丄恾傛傝懱愊傪媮傔傞偲丄
V=(1亊1亊1)+(2亊0.5亊0.5)+(4亊0.25亊0.25)+...
=1+0.5+0.25+.....
=2...嘐
傛偭偰丄亣=2...嘑
椉曈亣偱妱偭偰丄
1=0...嘒
椉曈偵1傪懌偟偰丄
2=1...嘓
Q.E.D. 徹柧廔椆
摉慠偙偺寢壥偼偍偐偟偄偱偡偑丄偙偺傛偆側寢壥偵側偭偨尨場偼偙偺徹柧偺偳偙偱偟傚偆偐丅偦偺売強傪嘆偐傜嘓偺偆偪堦偮慖傫偱壓偝偄丅
壣側恖偼棟桼傕偍婅偄偟傑偡丅
掲傔愗傝偼堦廡娫丅
捛婰
惵偺柺愊偲愒偺柺愊偺搑拞寁嶼偑晛捠偵娫堘偊偰偨偺偱廋惓偟傑偟偨丅偡傒傑偣傫丅摎偊偼曄峏側偟偱偡丅